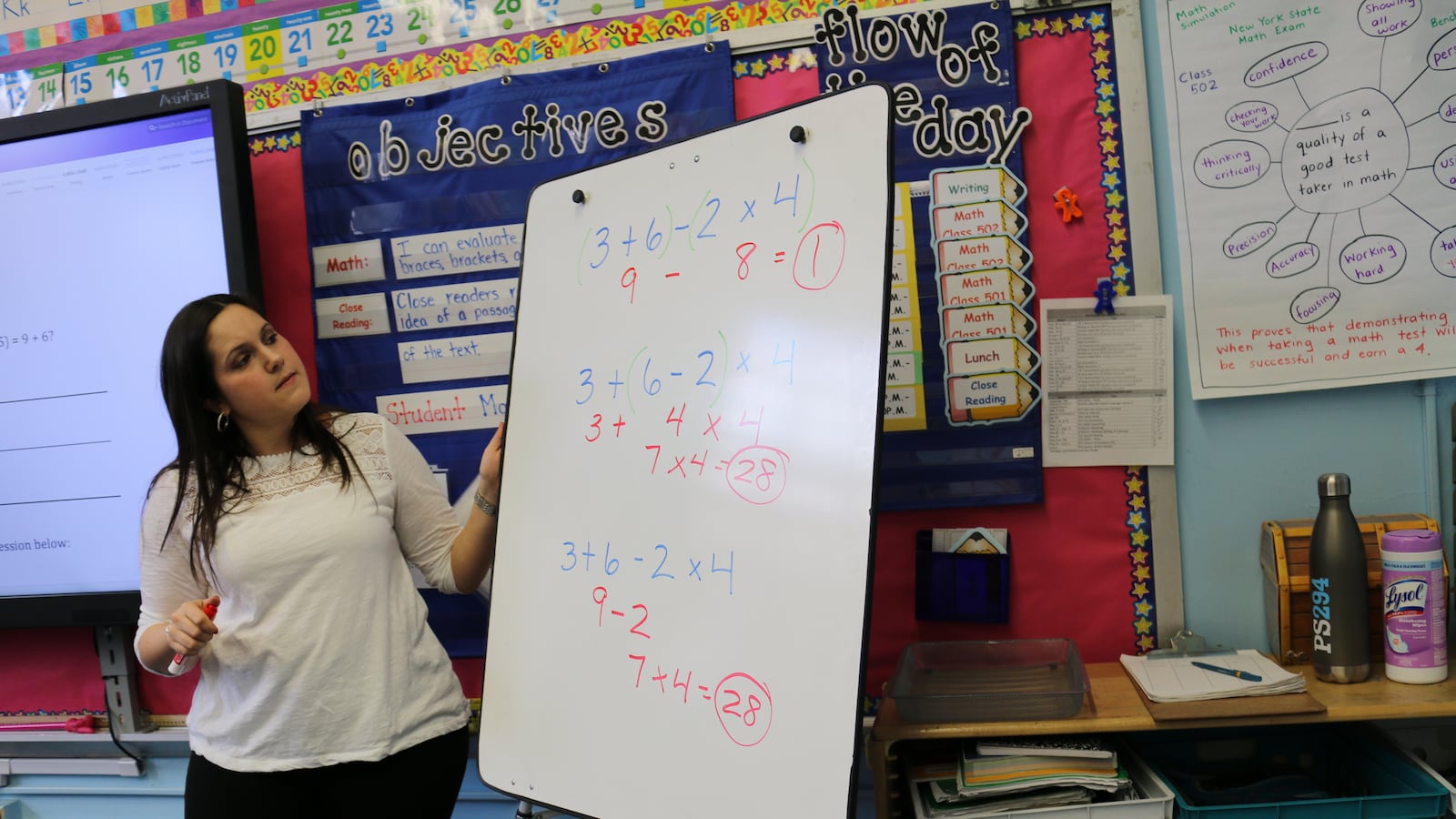At P.S. 294 in the Bronx, math is often a matter of debate.
In Nicole Lent’s fifth-grade class, groups of students take turns explaining how they solved the math problem of the day, respectfully disagreeing or enthusiastically lending support to their classmates’ arguments.
Lent floats around the room, asking probing questions but stopping short of revealing the right answer — opting to let students figure it out together instead.
“I always thought you had to teach the easiest way to just get an answer, and that is not the case,” she said. “I wasn’t giving them the opportunity to think critically about the problem and explore it in different ways.”
Lent is one of a team of teachers at P.S. 294, The Walton Avenue School, who focus only on math instruction. The city Department of Education has encouraged elementary schools across the city to take the same approach, called “departmentalization,” as part of its Algebra for All initiative. By placing the most capable teachers in charge of math instruction in fifth grade, the city hopes all students will be able to pass algebra by their first year of high school.
P.S. 294 has embraced the shift, starting departmentalized math instruction even earlier — in third grade. That’s in addition to its discussion-based approach. Lent has had a role of ushering both changes into the classroom.
She began using math debates and discussions after visiting another school that used the same model, and feeling struck by what she saw.
“I just remember going to those classrooms and thinking it was the coolest thing to see kids having a discussion,” about math. “I was just like, ‘How do I get my kids to do that?’”
The answer came through professional training offered by the city, along with picking and choosing the teaching resources that worked best for her needs. Soon, Lent’s new method spread throughout the school.
Now, half her time is spent in the classroom, and the rest of her day is spent working with her fellow math teachers as an instructional coach. She visits classrooms and regularly welcomes teachers into her own, all in an effort to provide constructive feedback, troubleshoot lessons and perfect new teaching strategies.
“It’s a different type of rewarding experience than working with children, but you see the same kind of growth,” she said. “We’re always working together to drive our instruction.”
This interview has been condensed and lightly edited.
Why did you become a teacher?
I never saw myself at a desk job where every day was the same. The great thing about teaching is that every day is different and truly rewarding, as you get to see your students grow and show progress over an extended period of time.
What does your classroom look like?
The students are the focal point of the room. You won’t find a teacher’s desk in my room. Around the perimeter are bookshelves containing student supplies … and “anchor charts” for students to reference … One example of an anchor chart would be to have the steps to adding fractions with unlike denominators, with the example of each step written out.
Students are permitted to get up at any time to access the supplies they need without asking for permission. We have set the expectation that they are in charge of their own learning and can self-assess when they need a resource to help them persevere through math tasks.
You had to learn a whole new way to teach math. What was the hardest thing about making that shift?
The hardest thing for me when making the shift from a teacher-led classroom to an approach that’s based on student inquiry and discussion was a shift in teacher mindset so as not to associate student conversation with off-task behavior.
What advice would you give to school leaders or teachers who might be considering departmentalizing math instruction?
I would advise them to start small and pilot departmentalizing on one grade first to see if it’s something they want to invest in doing at additional grade levels. We did this at P.S. 294, when I taught fourth grade last year, and it was very successful. We were able to work out any challenges and adjust what was necessary because we started small. At P.S. 294, we are now departmentalized on grades 3-5 for both [English Language Arts] and math. Teachers now receive the support they need and are focused on the content area they teach and have become true experts in their practices.
Fill in the blank. I couldn’t teach without my _____________.
I couldn’t teach without my computer because technology now plays a crucial role in education. Without my computer I wouldn’t be able to play instructional videos for my visual learners or have students come up to the Promethean board (an electronic whiteboard) and manipulate math content, which plays a pivotal role in assisting them in understanding math content.
What is one of your favorite lessons to teach? How did you come up with the idea?
One of my favorite lessons to teach this year was on division of fractions. I always thought we had to teach it using the strategy I learned as a child known as “keep, change, flip.” That’s a strategy used to solve an expression such as 1/4 divided by 3. You would keep the fraction, change the sign from division to multiplication, and flip the whole number from 3 to a fraction of 1/3. The quotient is 1/12.
I didn’t know exactly why this strategy works, I just knew it did.
After attending one of the Algebra for All professional developments last summer, I learned from a colleague at another school how to use visual models: We draw three “wholes” and divide each whole into fourths. The quotient is one piece out of the twelve total pieces you have from all three models (wholes you drew). We ask the students to think about the question: “How many fourths fit in three?” When it came time for me to teach them to my students this year, I knew exactly how to show them to divide fractions by whole numbers and by fractions in a purposeful and meaningful way.
How do you respond when a student doesn’t understand your lesson?
After a quick check for understanding that takes place after my mini-lesson, students who don’t understand my lesson meet in a small group with me on the carpet, while the rest of the students engage in differentiated math tasks on their level independently at their seats. During this time, I reteach students using a different method than the first time. This includes the use of manipulatives, instructional videos, and whiteboard work. Once I re-teach the concept using a different strategy, I conduct another quick check to see if they mastered the concept, and if so, they then go off independently to try some math tasks on their own.
How do you see your role as an instructional coach? What do you think is the most effective way to help other teachers improve their practice?
My role as an instructional coach is to build capacity across the school in the area of math instruction. Ultimately this means pushing practices down: taking the rigor and instructional approaches used at the 3-5 level and adjusting them to be used at the K-2 level according to the students’ individual needs.
The most effective way to help other teachers improve their practice is to hold debrief sessions following classroom visits, co-teaching sessions, or modeling lessons in their classroom, and providing actionable feedback that they can implement immediately.
What’s your go-to trick to re-engage a student who has lost focus?
Oftentimes, it takes some time to realize a student is lost and you don’t know exactly where they began to get lost. To avoid guessing and confusing them some more by repeating the last thing I said, I will restart and go step by step from the beginning while having that student assist me. Engaging the student along with the teacher has been the best strategy because you know they are listening and following along, because they are personally and directly involved with the teacher.
Your school has a common planning period. Has that helped change the way you teach?
Common planning periods bring teachers together to learn from one another and collaborate on projects.
During a recent common planning session, we had a consultant from Silicon Valley come and teach us about the difference between re-teaching vs. re-engagement lessons. Re-teaching lessons teach content again to a group of students who didn’t master it the first time. Re-engagement lessons allow students to work with a task to build mathematical ideas.
He showed us the data surrounding re-teaching vs. re-engagement lessons, which indicated that re-engagement lessons are what build students’ critical thinking skills. I realized that instead of having re-teach lessons built into my math block each day, that it would be much more beneficial to my students to participate in re-engagement tasks more often, as research had shown that that’s what truly pushes their levels.
Tell us about a memorable time — good or bad — when contact with a student’s family changed your perspective or approach.
A few years back, one of my students who had always been a Level 4 student [top-scoring on state, city and school assessments] started to act out in negative ways, not complete her homework, and be disruptive during lessons. After several warnings, I decided to call home to speak to the parent to notify the parent as to what was going on. As it turned out, this student’s father had recently moved out of state as the parents were getting divorced. Her mother said she was not taking it well and was acting the same way at home.
I asked the student to stay with me during her recess and spoke to her about what was going on at home. After some time, she finally opened up to me and let me know about her parent’s divorce.
We shared our own personal stories, and I was able to connect with my student on a much deeper level, and let her know that I am here for her any times she needs an ear to listen. From that day on, the student confided in me as she needed to and improved her effort and behavior in the classroom.
What’s the best advice you ever received?
A colleague told me that, “As educators, we learn best from our students.” I thought that had been the silliest thing as I had considered myself the head of the classroom who was supposed to know everything. As I began to dive deeper into my career, I couldn’t agree with her more.
My students have taught me that teaching is not black and white. There is no perfect science to it. Everything we do as educators is based off of what our students know and do, resulting in continuous reflections on our own practices. What needs to be modified? What needs to be revisited the following day? What shouldn’t be done anymore? What can I do further to push or help my students? What worked and what didn’t work? [These] are things we reflect about regularly. My students are the reason my toolbox of promising practices is so strong.
To read more stories in the How I Teach series, click here.